Knots and links
| Knots and links | |
|---|---|

| |
| On display at | Museo de Matemáticas Monasterio de Casbas |
| Type | Hands-on, riddle |
| Topics | Topology, knot theory |
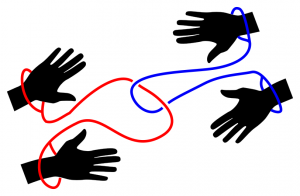
Knots and links is a riddle game used in the Museo de Matemáticas Monasterio de Casbas. In the game, two people are "handcuffed" with two ropes and have to release themselves. A physical model displayed next to the visitors gives a hint.
Description
The game only needs two ropes for the people to interact. Additionally, a wooden model serves as hint and explanation.
To set up the game, the mediator picks two visitors and ties them according to the figure: each visitor has both hands tied together with a rope that surrounds each wrist. The loop around the wrist closes with a tight knot, but leaves some space between the wrist and the rope, although not enough to slip the hand off. The two visitors are attached together because their chest, arms, and rope make two linked rings. The goal is to unlink themselves without untying the knots around their wrists.
The wooden model is a frame (such as a box without front and back walls), from the bottom side a stick goes towards the center, and holds a ring. This stick with ring has the shape of an eye bolt. A second stick goes from a side wall towards the center and penetrates without touching the ring sustained by the first stick. The first stick represents the rope with the loop around the wrist, and the second stick represents the arm.
After playing around for a bit, the mediator uses the wooden model as a hint: it explains what the sticks represent, and puts another rope on the model, as it is in the real situation. It becomes apparent that the solution comes by using the space between the loop and the wrist.
Activities and user interaction
The mediator sets up the situation and the two visitors need to think together. It works great with children or adults, and the situation is likely to become a tangle, and laughs are assured.
The wooden model really helps to the reflection of what does it mean to be linked; mathematically, the two visitors are never linked. It also helps to find the solution by reflection and not by blindly trying to move things around.
Mathematical background
Topology remains a big unknown domain for most of the general public, which will ask why that is mathematics. Topology is a branch of mathematics that deals with deformation of objects, without attending to measurement of any distance. Knots are such objects: it is not important how long are the ropes, or if they are straight or curved, just matters the connectivity between the links.
But without telling the visitors that there is a branch of mathematics to study knots, just the fact that one has to make reasonings, and define precisely what does it mean to be linked, makes them see that it is related to mathematics.