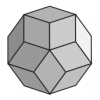
Ammann rhombohedra
| Ammann rhombohedra | |
|---|---|

| |
| On display at | Deutsches Museum |
| Type | Hands-on, puzzle |
| Topics | Polyhedra, tilings |
The Ammann rhombohedra is a hands-on puzzle exhibit on display at Deutsches Museum.
Contents
Description
Puzzle. A set of 20 wooden pieces needs to be put together. The pieces are called "golden rhombohedra" or "Ammann rhombohedra". There are two types of those pieces, and 10 pieces of each type, but all of them are polyhedra consisting of six rhombic faces. All the faces of all the pieces are equal (a golden rhombus). The goal is to combine them into a “ball” (rhombic triacontahedron). The label at Deutsches Museum reads:
Instructions:
The wooden Ammann Rhombohedra has to be put together into a ball. View from above:
A polygonal cup with the appropriate dimensions helps to support the construction.
Activities and user interaction
The typical user will understand quickly the goal and will spend a good amount of time trying to solve the riddle.
Many other constructions are possible using the golden rhombohedra (or Ammann’s rhombohedra), so other challenges could be added. Furthermore, it would be a nice addition to have a panel mentioning Ammann’s aperiodic tilings, similar to Penrose ones.
Mathematical background
The faces of these rhombohedra pieces are golden rhombi, that is, a rhombus whose diagonals are in the golden ratio φ = (1+√5)/ 2. There are two types of pieces that one can construct from them: the acute form, in which there are two opposed vertices where three acute angles meet; and the obtuse form, where there are two opposed vertices where three obtuse angles meet.
These golden rhombohedra have rich combinatorial possibilities, for instance, one can make the rhombic triacontahedron (ball-like) or the rhombic hexecontahedron (star-like).
Besides the puzzle, it is very interesting its link with aperiodic tessellations. Penrose tilings of the plane are widely known, and in fact, many math museums have an exhibit based on one of Penrose's designs (although they usually lack an explanation of what is the Penrose aperiodic tiling). Less known are the Ammann tilings, and in particular, Ammann’s aperiodic tiling of the three-dimensional space. Ammann tiling is such that by adding some “notches” or gluing rules to the faces of the two rhombohedra, one can obtain a space-filling tessellation of the space, which is non-periodic. It would be a perfect companion to a plane Penrose tiling exhibit.
History and museology
The rhombic triacontahedron was discovered and studied extensively by Kepler in his Mysterium Cosmographicum (1596).
The first use of the solid as a recreational puzzle using this dissection into golden rhombohedra is by German mathematician Gerhard Kowalewski, in his book Der Keplersche Korper und andere Bauspiele (1938) (Construction games with Kepler's solid).
Robert Ammann's discovery of the aperiodic tiling of the space using golden rhombohedra is from the 1970s. Using the Ammann name for this exhibit seems to be honorific.
Resources
Translation of Kowalewski's 1938 book:
- Gerhard Kowalewski and David Booth, Construction Games with Kepler's Solid, Parker Courtney Press, 2001. https://www.zometool.com/content/KowalewskiWeb.pdf.
Construction by George Hart and Elisabeth Heathfield:
An article about Robert Ammann worth reading in connection to this exhibit:
- Marjorie Senechal, The Mysterious Mr. Ammann, The Mathematical Intelligencer, 26 (4): 10–21, 2004. doi:10.1007/BF02985414, MR 2104463.