Polyhedral kaleidoscopes
| Polyhedral Kaleidoscopes | |
|---|---|

| |
| On display at | Museu de Matemàtiques de Catalunya |
| Type | Hands-on |
| Topics | Mirrors, symmetry, polyhedra |
Polyhedral kaleidoscopes is an exhibit on display at Museu de Matemàtiques de Catalunya (MMACA).
Contents
Description
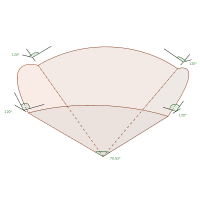
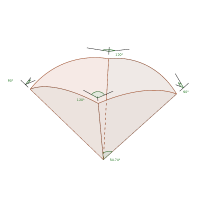
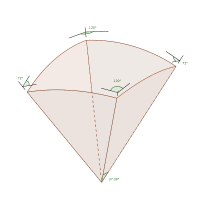
The exhibit consists of a set of three spherical kaleidoscopes. For each kaleidoscope, four equal mirrors in the shape of circle sectors are arranged on an inverted rhombic pyramid structure. A set of colored wooden pieces accompanies each kaleidoscope so that these pieces fit inside the mirrored pyramid. As a result of the reflected piece, one sees several kinds of symmetric polyhedra. Each kaleidoscope has a different set of symmetries, depending on the dihedral angles of the mirrors. Those are (120,120,120,120), (120,90,120,90) and (120,72,120,72) degrees, giving locally at each edge dihedral symmetries of order (3,3,3,3), (3,4,3,4) and (3,5,3,5) respectively. The four mirrors on each kaleidoscope are equal, and they span a circular sector of angle 70.53º, 54.74º, and 37.38º respectively.
Materials: Mirrors are glass-made, glued over plywood. Colored pieces made of MDF wood with tinted wax.
Activities and user interaction

The activities adapt to the age and background of the visitor. For younger visitors (5-10 years old), it is sufficient to bring them the wooden pieces and let them discover the beautiful shapes that are obtained. Next, play to identify the shapes with the list of polyhedra on the wall.
For an intermediate level, one can challenge them to tell in advance which of the polyhedra on the poster will appear when putting a wooden piece inside the kaleidoscope, and induce them to see the number of copies seen at each corner. This number of copies around the edge of the kaleidoscope depends on the angle of the two mirrors meeting at this edge. Discuss why the three different kaleidoscopes give rise to three families of polyhedra.
For advanced visitors, one can discuss the notion of group and symmetries. Each family of polyhedra share a symmetry group, which is generated by the reflections on the mirrors. This way, one see that the abstract concept of symmetry is related to the structure that provides the kaleidoscope, but the actual shape depends on the particular piece that we put inside, that can be one of the wooden pieces or any object.
Mathematical background
Depending on the definition we choose, we can make lists of hundreds of polyhedra, grouped by different characteristics. Here we see that more important than the number of faces, or their shape, a much more significant feature is which symmetries does it has. All the polyhedra that fit on one of the kaleidoscopes share the same symmetries, which are different from those of another kaleidoscope. A symmetry in this context is a movement that one can do and leaves the polyhedron unchanged (for instance rotating a cube a quarter of turn around the line that crosses two opposite faces by their centers). For polyhedra, symmetries can be rotations or reflections. A polyhedron can be embedded into a concentric sphere, and all the symmetries of the polyhedron are movements of the sphere. The angles of the mirror circular sectors relate to the dihedral angles by spherical trigonometry. Similar relations are needed to calculate the bevels on each face (wooden pieces). The set of symmetries of a polyhedron has the mathematical structure of a group. Groups can be studied abstractly, but here we find a perfect application of group theory to geometry. One can mention that all these groups of kaleidoscopes are generated by order 2 elements, and hence are Coxeter groups, which are completely classified.
History and museology
This exhibit has become an iconic feature of MMACA, and it is usually part of MMACA’s travelling exhibitions. Although there are precedents (Matemilano exhibition, Milan, Italy, 2003-04), this exhibit does not use the minimal set of three mirrors to generate the polyhedra, but sets of four mirrors and symmetric wooden pieces. This has the advantage of being stable (the pieces hold in place) and the aperture of the basket is bigger, trapping light and offering a good view of the polyhedra. It is believed to be the first exhibit with this four mirrors design.
The exhibit was designed and built by Josep Rey for MMACA. Rey presented the exhibit at the JAEM conference (Spain, 200?) with a set of didactic activities.
Similar exhibits
Similar kaleidoscopes can be found at Erlebnisland Mathematik (Germany), Le Labosaïque (France), and Atractor (Portugal).
Resources
The following books are a good source for constructing kaleidoscopes:
- M. Wenninger, Spherical models
- H.S.M Coxeter, Regular polytopes
See also