SURFER (IMAGINARY exhibit)
| SURFER | |
|---|---|
| |
| On display at | IMAGINARY exhibitions and others |
| Type | Software |
| Topics | Algebraic geometry, surfaces |
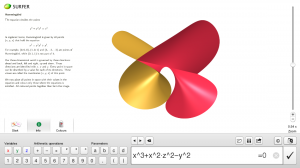
SURFER is a software exhibit used and developed by IMAGINARY. This program draws algebraic surfaces in 3D in real time, from a polynomial given by the user as the input. Some example surfaces, parameters and colouring allow interactive play with the surfaces.
Description
The main and only window of the program has a view of the current algebraic surface, which one can drag to rotate and zoom. The lower part of the window has a small keyboard and a textbox with the polynomial defining the surface. With the on-screen keyboard, the program is ready to be used on touchscreens without physical keyboard. A left menu brings some options of colouring and a list with some examples of surfaces. Each surface is accompanied of an explanation text. The program is available in 15 languages.
Optionally, two buttons can be activated: one for saving the surface in a file, and another for printing the surface to bring it to the visitor. These features can be used to organize competitions amongst visitors and schools for obtaining the most beautiful surfaces.
Activities
On exhibitions, SURFER is displayed usually in a big touch screen, and often surrounded by big posters of algebraic surfaces that can be produced with the program. On free-visit exhibitions, visitors can discover the features of the program exploring by themselves, and the on-screen keyboard invites to write and change the equations. However, this exhibit usually poses a difficulty barrier to casual visitors, so the presence of a mediator is highly advised. A mediator can present the main features of the program and give a general overview of what is algebraic geometry in about 10 minutes, for instance gathering 4-6 people at a time. See the Video Tutorial above for an example of such presentation.
SURFER can be used also in longer workshops (up to 1 or 2 hours), at museums, schools or public places equiped with the necessary resources, namely a computer for each participant and a screen/projector for the mediator. On these workshops, the participants are guided on a tutorial, leaving them to explore the equations. The mediator proposes challenges of increasing difficulty, like "draw three spheres", "draw a snowman", etc. On these activities it is useful to use a shared text editor along with SURFER to prepare the equations before drawing them, and to share equations between the mediator and the participants.
Background
Algebraic surfaces are sets of points (x,y,z) in space that satisfy a given polynomial equation p(x,y,z)=0. The extensive texts on the program provide enough information as to get a general idea on the subject. Additionally, the Video Tutorial and the Didactical guides on the SURFER website give enough resources for the training of mediators. Deeper insights on Algebraic Geometry will probably need a more formal training in higher mathematics.
On the technical side, visualization of algebraic surfaces can be tricky. Most surfaces appearing in computer graphics are (ideally) smooth surfaces, that can be approximated by a triangulation mesh with quite good accurary. This mesh consist on a vast collection of flat triangles in space, and graphic cards are designed to render them rapidly on screen. However, many interesting algebraic surfaces contain mathematical singularities (points where the surface fails to be smooth), and the triangulation technique is not a good approach. A different technique in computer graphics is ray-tracing. On this technique, one describes a scene abstractly (objects, lighting, textures, and a camera view), and the rendering consists on tracing, for each pixel on the final image, a light ray from the camera, inciding on the closest surface, and reflecting according to the laws of optics to reach the source of light, and this determines the colour of the pixel. Ray-tracing is much more expensive int terms of computation power and usually is only used for still images, whereas triangulation can be used in real-time video such as videogames. SURFER is a ray-tracer optimized for rendering algebraic surfaces in real time.
History and museology
The first antecedent of SURFER is the program surf [1], released in 2000 by Stephan Endrass and others. This program is a script-driven ray-tracer designed for algebraic surfaces written in C++. In 2006, Herwig Hauser designed and formulated a gallery of algebraic surfaces for the ICM 2006 in Madrid. That gallery was created using POV-ray, a general purpose ray-tracer software that, unlike most other ray-tracers, admitted as a primitive shape an algebraic surface defined by the zeroset of a polynomial. At that moment, no program was fast enough to render live a surface.
The IMAGINARY project was created with occasion of the German Year of Mathematics 2008, and one of its core initiatives was to design a fast renderer of algebraic surfaces with a simple user interface to be used in an exhibition. Firstly, the old surf program was ported to Java libraries, giving rise to jsurf. Then, a complete user interface was designed and the result was SURFER 2008. This was the version used in the German exhibitions during 2008, and included several advanced features as well as a more simplified view.
In 2010 the user interface was redesigned, including several more examples of surfaces (such as Hauser's designs and record singularities surfaces). Some features such as multiple surfaces and animation were removed, in order to have a much simpler interface for exhibitions. This is the current version of SURFER.
In 2012, the National Museum of Mathematics and IMAGINARY made an agreement to design a new exhibit based on SURFER, Formula Morph, that is currently on display at MoMath. This exhibit has an user interface based on physical devices (wheels, buttons, levers) which are mounted on the exhibit structure that holds the screen.
